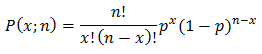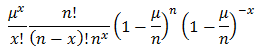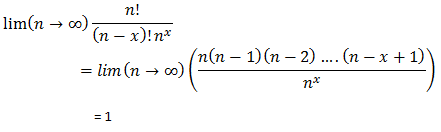Part 1 of Statistics within Capacity Management and Performance Engineering Series.
Within this series I will be exploring the nature of statistical analysis within the world of Capacity and Performance Management. You can create as many pretty graphs and make wide ranging statements that effect the decisions of management but if you don’t know what is actually going on, then true understanding will always elude you. Herein an attempt is given to educate those lacking the formal education required.
The first piece for discussion is what is frequently termed Poisson distribution; what is little known is this is formulated from a limiting condition of binomial distribution. Binomial distribution defines the discrete probability, P, of x successes in a sequence of n independent yes or no experiments, each of which yields success with probability p.
The advantage of using poisson distribution is that n or p do not need to be known! This can make assumptions much easier.
It is summed up neatly in the following equation:
(1)
If we add the following limiting cases:
And observing that:
It is clear that p must tend to 0. Using these it allows us to reduce the equation (1) to reflect this.
What’s interesting here that we can now apply the limiting constraints above to (4) to allow a much simpler evaluation.
This then allows us to get to the conclusion that: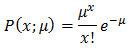
Which conveniently is the equation for Poisson distribution!!
Now that we have explored how to generate the equation for Poisson distribution, we are able to take this and prove that n or p need not be known. In the next instalment we will prove this, allowing full comprehensive understanding of the topic. Hopefully greater understanding of a mathematical tool has been shown and you can, without fear and with full understanding, understand Poisson distribution next time you encounter it.