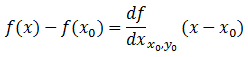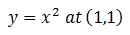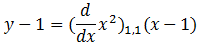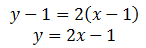Part 3 of Statistics within Capacity Management and Performance Engineering Series.
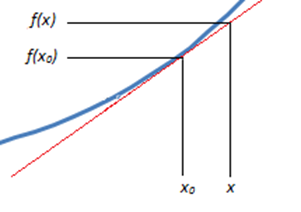
Having spent the past 2 weeks within the world of probability and distributions a change was necessary. Herein we will be discussing linearization. Let’s assume you have plotted a trend and it is not linear, how can you interpret this and make a prediction from this?
Let’s assume we have a function of one variable (these principles can be expanded for multivariable systems):
This is easily manipulated within our example. Let us consider a point on the this line (x0,f(x0). We know this point and we want the approximation at (x,f(x)). With this little information we can make a linearization of the curve.
With observation it is clear that the linear approximation then follows the form of:
This is rather convenient as it matches the form of a linear function. The approximation is said to be exact at the point at which it is defined (x0,f(x0)). The further from this point the approximation needs to be treated with caution.
Example
Using (2) and substituting the values:
And now we can simplify:
Thus we now have a linear approximation at the point 1,1 for y=x2 using this we can now make an approximation. Let’s assume we want to know what the value of y will be when x is 1.1. The approximation gives 1.2, while the actual value is 1.21. Our approximation falls within 1% of the actual value. This is a powerful tool for making approximations close to a known value. And can provide a good estimate before much more complicated analysis is undertaken.